📖 서론
고등학교, 대학교 동안 그만큼 많은 문제를 풀어보고 자주 접한 함수들은 거의 대부분 연속시간$ ( $Continous Time, C-T$ ) $함수들이다. 그래서 sin(t), C-T 복소삼각함수인 $ sin(jw_0t) $, 더 나아가서 $ e^{jw_0t} $와 같은 함수들이 주기성을 갖는다는 것은 쉽게 받아들일 수 있다.
- 그런데 D-T와 관련된 함수들은 특이하고 낯설다. 모든 $ w_0 $에 대해서 주기함수인 $ e^{jw_0t} $와 다르게, $ e^{jw_0n} $은 주기함수일 수도 아닐 수도 있다. 이렇게 헷갈리는 주기성을 위주로 정리해보았다.
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- D-T 함수란? : 링크
❗줄임말
- D-T : Discrete-Time, 이산시간
- C-T : Continous-Time, 연속시간
1. D-T Complex Exponential의 형태

위의 항과 같이 자연상수의 지수에 $ jw_0n $이 올라가 있고, n이 변수(정수값만 가능)이다.
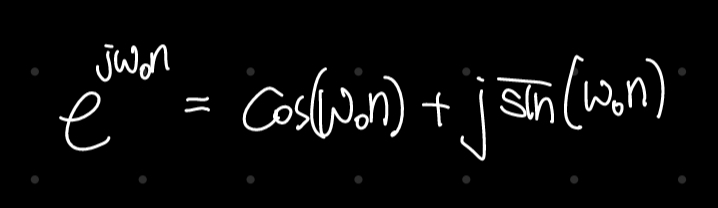
당연히 위와 같이 오일러 공식으로도 표현 가능하다.
2. 주파수$ ( $Frequency$ ) $
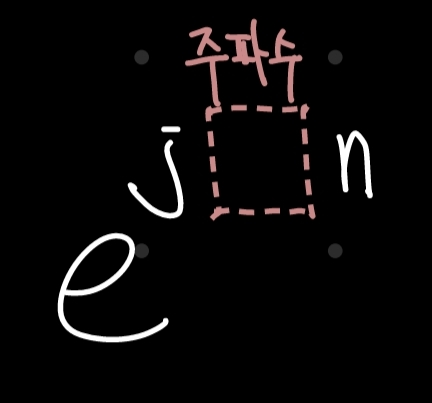
: 허수 j와 변수 n을 제외한 부분이 모두 '주파수$ ( $frequency$ ) $'인데, 아래 그림과 같이 '빨간색 네모' 자리에 들어가는 모든 것이 주파수라고 생각하는 것이 편하다.
- $ w_0 $이 주파수다라고 공식만 외우게 되면 $ e^{jkw_0n} $ 이런 꼴이 나올 때 간혹 헷갈린다.
- 주파수는 '실수'이다.
복소수인 주파수도 존재하나..? 모르겠다
3. 주기성$ ( $Periodicity$ ) $
: 보통 D-T에서는 주기를 N이라 한다. $ ( $C-T에서 T라고 하는 것과 대조적$ ) $
- D-T Complex Exponential 중 주기를 갖는 것은 일부에 불과하다!!!
- 즉, 특정한 조건을 만족해야지만 주기성을 갖는다. 이 특정한 조건은 <4. 주파수와 주기성의 관계>에서 다룬다.
4. 주파수와 주기성의 관계
4.1 D-T 복소지수함수가 '주기함수'이기 위한 '주파수'의 조건
만약 D-T 복소지수함수가 주기함수라면, 주기 N과 주파수 $ w_0 $의 관계는 다음과 같은 식을 만족한다. 이때 m은 정수이다.
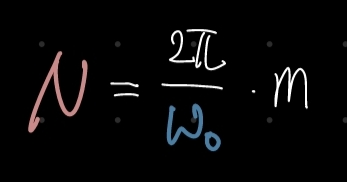
N은 자연수이므로(D-T 함수의 주기는 당연히 자연수다!!) m의 역할은 아래와 같다.
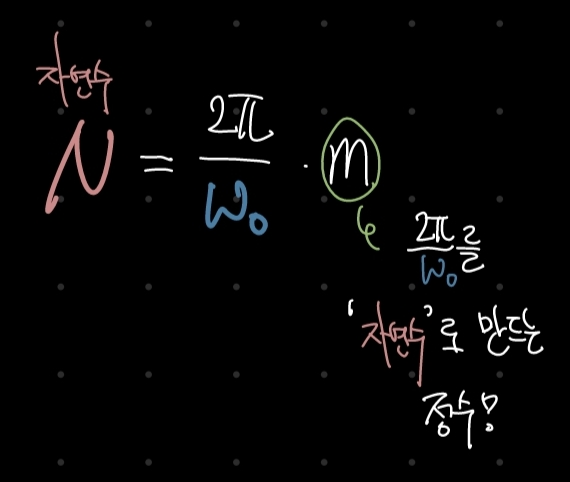
m에 의해 $ ( 2{pi}/w_0 } $가 자연수가 되기 위해서는 $ ( 2{pi}/w_0 } $

'전기전자 과목 | 콘텐츠 > 연결 중' 카테고리의 다른 글
| 디리클레 조건 (0) | 2024.10.21 |
|---|---|
| D-T 함수란? (0) | 2024.10.07 |
| 선형 시불변 시스템$ (Linear Time Invariant, LTI System) $이란? | Convolution의 쓰임 | (0) | 2024.10.06 |
| 푸리에 변환 공식 및 푸리에 급수의 직관적 이해 | 푸리에 급수에서 푸리에 변환을 이끌어내기 (0) | 2024.10.03 |
| C-T 푸리에 급수 (0) | 2024.10.03 |
📖 서론
고등학교, 대학교 동안 그만큼 많은 문제를 풀어보고 자주 접한 함수들은 거의 대부분 연속시간$ ( $Continous Time, C-T$ ) $함수들이다. 그래서 sin(t), C-T 복소삼각함수인 $ sin(jw_0t) $, 더 나아가서 $ e^{jw_0t} $와 같은 함수들이 주기성을 갖는다는 것은 쉽게 받아들일 수 있다.
- 그런데 D-T와 관련된 함수들은 특이하고 낯설다. 모든 $ w_0 $에 대해서 주기함수인 $ e^{jw_0t} $와 다르게, $ e^{jw_0n} $은 주기함수일 수도 아닐 수도 있다. 이렇게 헷갈리는 주기성을 위주로 정리해보았다.
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- D-T 함수란? : 링크
❗줄임말
- D-T : Discrete-Time, 이산시간
- C-T : Continous-Time, 연속시간
1. D-T Complex Exponential의 형태

위의 항과 같이 자연상수의 지수에 $ jw_0n $이 올라가 있고, n이 변수(정수값만 가능)이다.
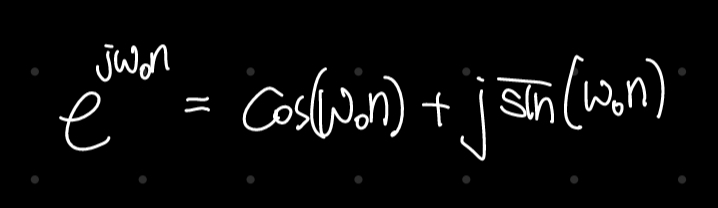
당연히 위와 같이 오일러 공식으로도 표현 가능하다.
2. 주파수$ ( $Frequency$ ) $
: 허수 j와 변수 n을 제외한 부분이 모두 '주파수$ ( $frequency$ ) $'인데, 아래 그림과 같이 '빨간색 네모' 자리에 들어가는 모든 것이 주파수라고 생각하는 것이 편하다.
- $ w_0 $이 주파수다라고 공식만 외우게 되면 $ e^{jkw_0n} $ 이런 꼴이 나올 때 간혹 헷갈린다.
- 주파수는 '실수'이다.
복소수인 주파수도 존재하나..? 모르겠다

3. 주기성$ ( $Periodicity$ ) $
: 보통 D-T에서는 주기를 N이라 한다. $ ( $C-T에서 T라고 하는 것과 대조적$ ) $
- D-T Complex Exponential 중 주기를 갖는 것은 일부에 불과하다!!!
- 즉, 특정한 조건을 만족해야지만 주기성을 갖는다. 이 특정한 조건은 <4. 주파수와 주기성의 관계>에서 다룬다.
4. 주파수와 주기성의 관계
4.1 D-T 복소지수함수가 '주기함수'이기 위한 '주파수'의 조건
만약 D-T 복소지수함수가 주기함수라면, 주기 N과 주파수 $ w_0 $의 관계는 다음과 같은 식을 만족한다. 이때 m은 정수이다.
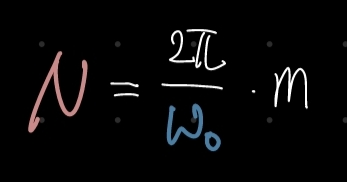
N은 자연수이므로(D-T 함수의 주기는 당연히 자연수다!!) m의 역할은 아래와 같다.
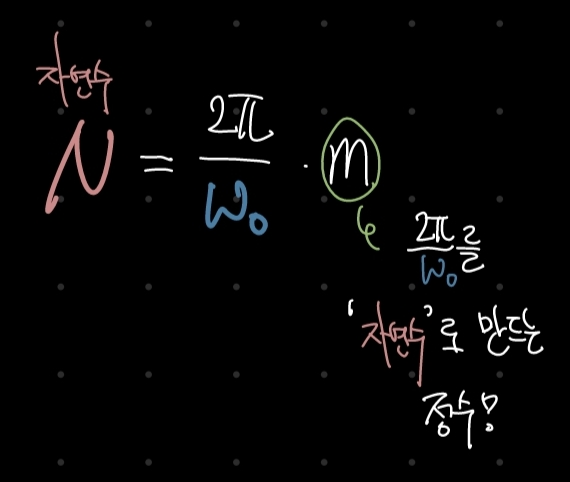
m에 의해 $ ( 2{pi}/w_0 } $가 자연수가 되기 위해서는 $ ( 2{pi}/w_0 } $

'전기전자 과목 | 콘텐츠 > 연결 중' 카테고리의 다른 글
| 디리클레 조건 (0) | 2024.10.21 |
|---|---|
| D-T 함수란? (0) | 2024.10.07 |
| 선형 시불변 시스템$ (Linear Time Invariant, LTI System) $이란? | Convolution의 쓰임 | (0) | 2024.10.06 |
| 푸리에 변환 공식 및 푸리에 급수의 직관적 이해 | 푸리에 급수에서 푸리에 변환을 이끌어내기 (0) | 2024.10.03 |
| C-T 푸리에 급수 (0) | 2024.10.03 |