📖 서론
- 컨볼루션은 다양한 분야에서 쓰이는 수학 연산자이다. 함수와 함수를 연산하여 새로운 함수를 만드는데, 그 방법이 수식만 봐서는 크게 와닿지 않는다. 이에 컨볼루션의 직관적인 의미, 성질들과 더불어 실제로 어떻게 손으로 계산하는지에 대하여도 최대한 직관적으로 정리하려고 노력했다.
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- 이상적분
- 무한급수
- LTI 시스템 : 3.2절에서만 필요함, 링크
❗줄임말
1. 정의
1.1 컨볼루션 합$ ( $Convolution Sum$ ) $의 정의

Convolution sum은 기호 * 로 표시되며, 위와 같은 식으로 표현된다.
a와 b를 convolution sum한 결과를 C[n]이라고 하면, C[3]과 같은 특정한 값을 구하기 위해서는 아래와 같은 무한번의 곱과 합이 필요하다.

이렇게 하나의 함숫값을 구하는 데에도 무수히 많은 양의 연산이 필요한데, C[n]의 모든 함숫값들을 알는 것은 불가능 하지 않을까라는 생각이 든다. 다행히도 a[n]혹은 b[n]이 (혹은 둘 다) 일부 구간을 제외하고는 함숫값이 0인 경우가 대다수이기 때문에 할 만하다. 실제 함수들에 대해서 어떻게 계산하는지는 <4. 계산팁> 에서 다룬다.
1.2 컨볼루션 적분$ ( $Convolution Integral$ ) $의 정의

Convolution Integral 의 기호도 마찬가지로 * 이다.
실제 함수들에 대해서 어떻게 계산하는지는 <4. 계산팁> 에서 다룬다.
2. 직관적 이해 - 3Blue1Brown 유튜브, 혁펜하임 유튜브
2.1 3Blue1Brown 유튜브 : k축에서의 이해
컨볼루션을 하기 위해서는 하나의 함수를 뒤집은 다음에 다른 함수와 곱하기를 하는데, 이 뒤집는 이유에 대해서 주사위를 이용한 확률분포적인 관점에서 설명을 해준다. 이 과정에서 convolution의 결과가 의미하는 바 또한 직관적으로 보여준다.

- CNN$ ( $Convolution Neural Network$ ) $에서 convolution을 할 때 굳이 왜 뒤집는지 의문이 들었는데, 영상에서도 불필요한 행위로 보이는 이 점을 언급하며,
"In the computer science context, this notion of flippling around that kernal before you let it march across the original often feels really weird and just uncalled for, but again, note that that's what inherited from the pure math context, where like we saw the probabilities, it's an incredibly natural thing to do."
라고 확률분포 관점의 수학적인 의미를 생각해보면 좋다고 한다.
아래는 유튜브 영상으로 후반부에는 이미지 처리, FFT가 나오므로 흥미가 닿는데까지 보면 좋을 것 같다.
https://www.youtube.com/watch?v=KuXjwB4LzSA
2.2 혁펜하임 유튜브 : n축에서의 이해
LTI 시스템에서는 입력함수 x와 출력함수 y와의 관계가 y = x * h임이 알려져 있다. 이 식을 이끌어내고 이해할 때에 있어서 잘 생각을 해보면, 컨볼루션 연산자의 대상이 되는 함수 x와 함수 h를 뒤집은 적이 없다는 것을 알 수 있다. 그럼 3.1절에서 언급한 '함수를 뒤집는 이유'가 부정되는게 아닐까?라는 고민을 했었다.
이 고민에 대한 내 결론은
3.1절의 3Blue1Brown에서 함수를 뒤집은 이유는 k축을 기준으로 두 입력함수 a[k]와 b[n-k]를 바라보았고,
LTI 시스템에서는 n축을 기준으로 두 입력함수 x[k]와 h[n-k]를 바라보았기 때문이다.
아래의 Convolution Sum 공식을 다시 살펴보면, 오른쪽의 급수 부분의 a[k]b[n-k] 부분이
1. k축 기준으로, 둘 다 '함수'
2. n축 기준으로, b[n-k]만 '함수'이고 a[k]는 '함숫값'이다.

즉, a[k]가 '함숫값'이고, b[n-k]는 n축 기준 +k 만큼 평행이동한 '함수'인 것을 염두에 두고 혁펜하임 유튜브 영상을 보면 왜 LTI 시스템 공식을 이끌어낼 때 함수를 뒤집는 과정이 없는지, 혹은 함수를 뒤집는 과정이 없어도 이를 Convolution이라고 부를 수 있는지에 대하여 시원하게 이해할 수 있다.
LTI 시스템에서 n축 기준으로 convolution 공식을 유도해냈지만, 나중에 관련 문제들을 풀 때 거의 대부분 k축 기준으로 연산하게 된다. 유도해낸 LTI 입출력 식 자체가 convolution 그 자체이므로 n축으로 연산하던, k축으로 연산하던 전혀 문제가 될게 없다.
https://www.youtube.com/watch?v=uXl_QTsTj-w
3. 컨볼루션의 성질
4. 계산 팁 및 연습문제
4.1 Convolution Sum의 계산 팁
연습문제를 풀다 보니 Convolution Sum을 계산할 때에는 크게 세 가지 방법이 있는 것 같다.
- 방법1, 방법2 : convolution sum을 직접 계산할 때로, 우변의 무한급수를 계산할 때 'k축을 이용'하거나 'n축을 이용'할 수 있다.
- 방법3 : convolution의 성질을 이용하는 방법이다.
- 물론 성질만 이용하고 계산결과가 나오는 경우가 있는 반면, 성질을 이용하여 식을 간단히 만든 뒤 1번 혹은 2번의 방법을 쓰는 경우도 있다.
여기서는 방법1, 방법2만 정리하려고 한다.
$ ( $대부분의 문제들은 방법1로 해결하는 경우가 더 많은 것 같다. 다만 방법2로 풀면 간단한 경우가 있어서 구분해서 기억해두면 좋을 듯 하다.$ ) $

[방법1] k축 이용 : 뒤집고 곱하고 더하기!!
STEP1. b[k]를 y축 대칭이동하여 b[-k]를 만들어 놓는다.
- 그래프로 그려 놓으면 편하다. 그래프 그리기 까다로운 경우에는 식으로만 적어두어도 충분하다.
- 좀 더 간단한 함수를 b로 잡는 것이 편하다.
STEP2. n을 하나의 상수로 인식하여 b[n-k]를 상상한다. 이때 b[-k]를 k축 방향으로 n만큼 평행이동하면 된다.
- 모든 정수 n에 대하여 평행이동한 것을 모두 그리는 건 불가능하므로 상상만 한다.
STEP3. <STEP2>에서 상상한 b[n-k] 그래프와 a[k] 그래프(이때 그래프들의 가로축이 k이며, n을 하나의 상수로 고정했다는 것을 기억하자)를 벡터 내적하듯이 동일한 k 값에서의 함숫값들을 서로 곱한 뒤, 모두 더하는 행위를 할 것이다. 이 행위를 모든 n에 대하여 해야 하므로, 뭔가 곱하고 더하는 방식이 바뀌는 순간을 기점으로 n의 범위를 나눈다.
- 말로 표현하기 어려운데, 아래에서 예시를 보면 이해할 수 있을 것이다.
STEP4. 나뉜 n의 범위에 따라 곱하고 더한 결과를 적는다.
4.1.1 Convolution Sum 연습문제
문제

풀이
STEP1. b[k]를 y축 대칭이동하여 b[-k]를 만들어 놓는다.
- 그래프로 그려 놓으면 편하다. 그래프 그리기 까다로운 경우에는 식으로만 적어두어도 충분하다.
- 좀 더 간단한 함수를 b로 잡는 것이 편하다.
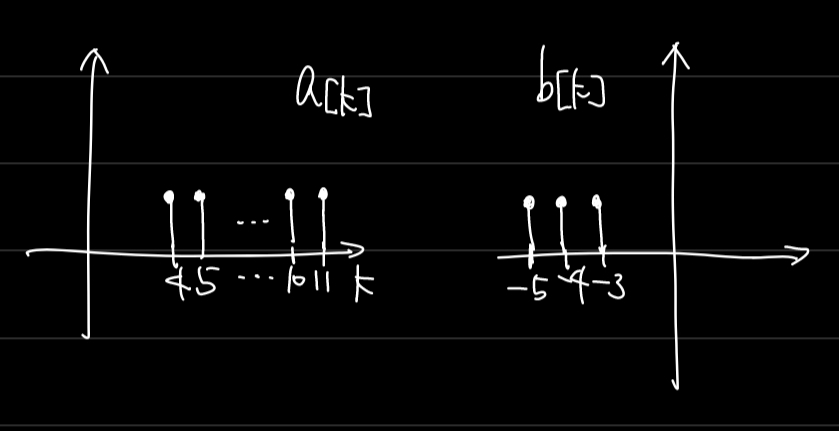
STEP2. n을 하나의 상수로 인식하여 b[n-k]를 상상한다. 이때 b[-k]를 k축 방향으로 n만큼 평행이동하면 된다.
- 모든 정수 n에 대하여 평행이동한 것을 모두 그리는 건 불가능하므로 상상만 한다.
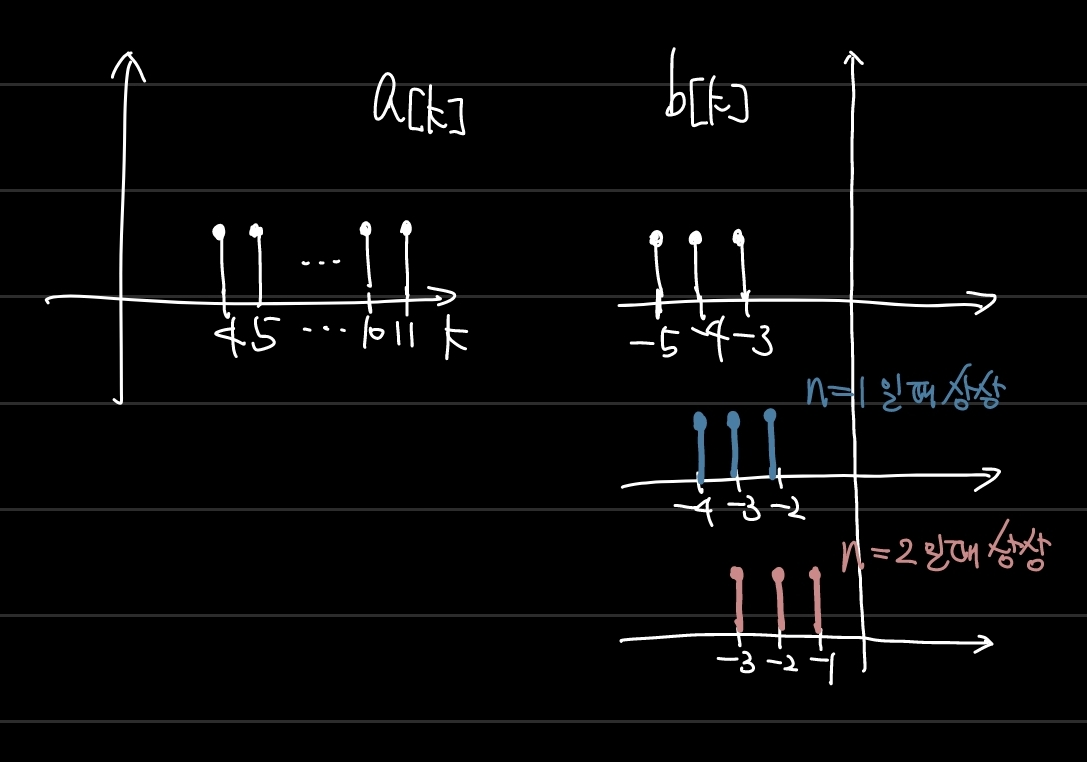
STEP3. <STEP2>에서 상상한 b[n-k] 그래프와 a[k] 그래프(이때 그래프들의 가로축이 k이며, n을 하나의 상수로 고정했다는 것을 기억하자)를 벡터 내적하듯이 동일한 k 값에서의 함숫값들을 서로 곱한 뒤, 모두 더하는 행위를 할 것이다. 이 행위를 모든 n에 대하여 해야 하므로, 뭔가 곱하고 더하는 방식이 바뀌는 순간을 기점으로 n의 범위를 나눈다.
- 말로 표현하기 어려운데, 아래에서 예시를 보면 이해할 수 있을 것이다.
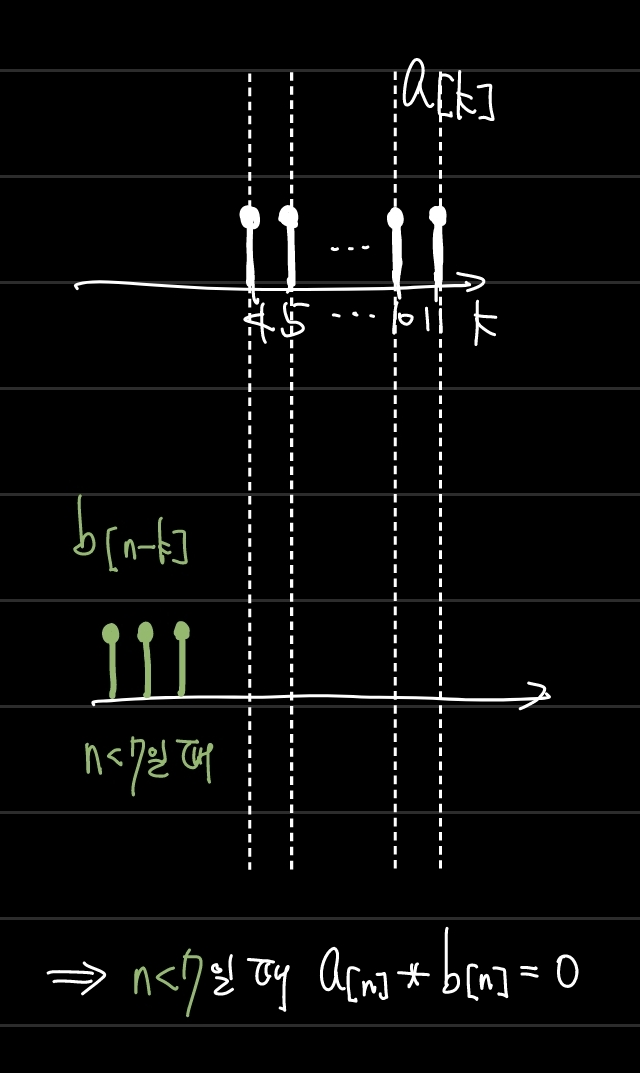
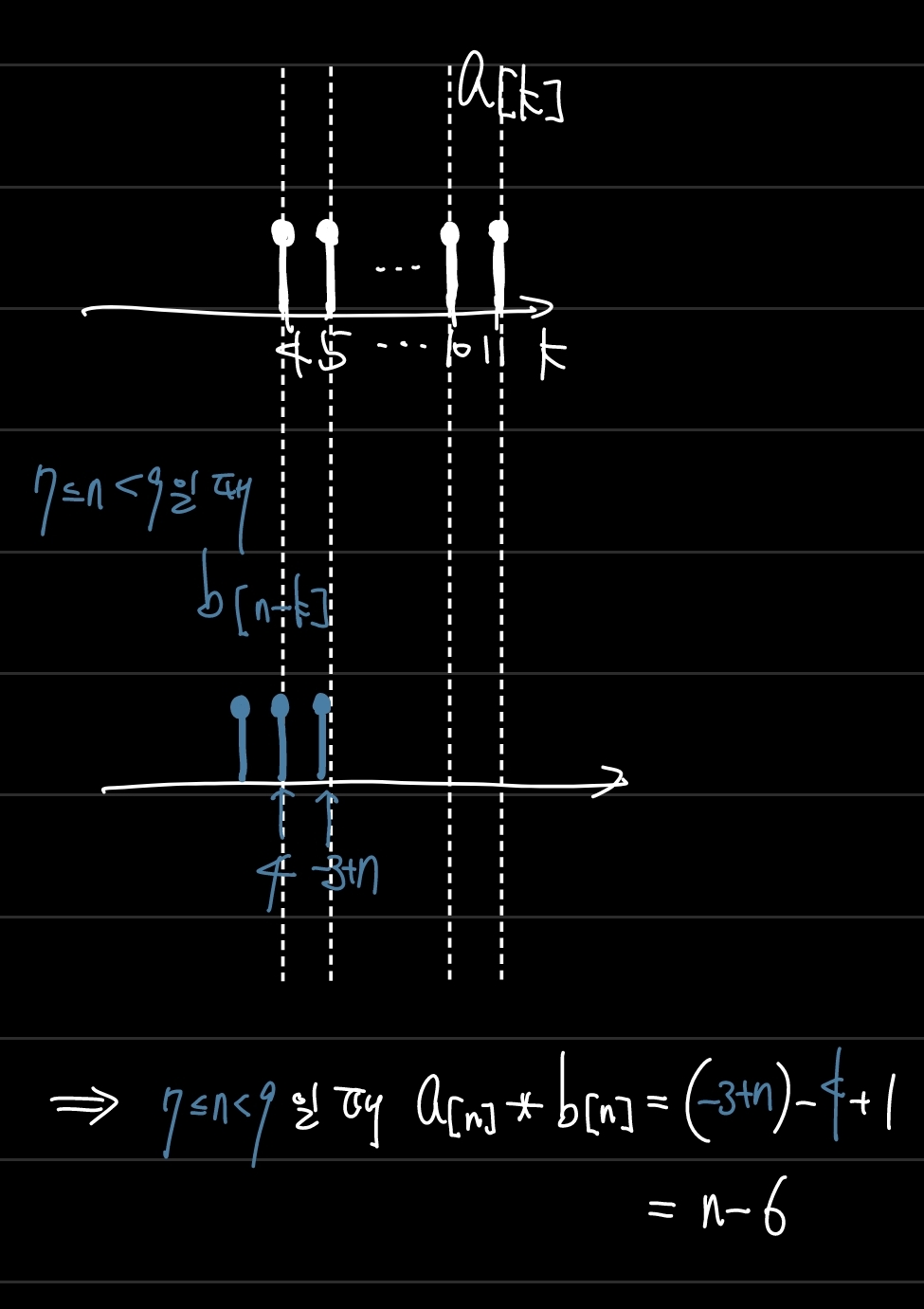
위와 같은 방식으로 n의 범위를 적절히 나눈 뒤, 겹치는 부분의 개수를 센다. 각각의 함숫값이 1이므로 겹치는 것의 개수를 세는 것으로 충분한 것이다. 만약 함숫값이 1이 아니면 곱하고 더하고 잘해야 한다.
STEP4. 나뉜 n의 범위에 따라 곱하고 더한 결과를 적는다.
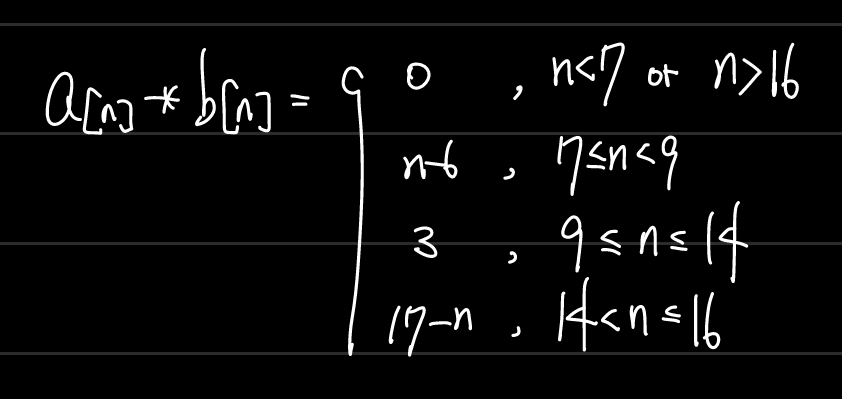
[방법2] n축 이용

무한급수를 전개했을 때, ..., a[-1], a[0], a[1], ... 이 함수가 아닌 '상수'임을 이용한다. [방법1]은 함수와 함수를 곱한 것을 상상해야하는 것과 다르게 지금 방법은 상수와 함수의 곱이므로 뇌를 반쯤 빼놓고 연산하면 된다.
- 그렇다고 b[n]을 계속 평행이동해야 하는 것을 잊으면 안된다.
# 연습문제
문제
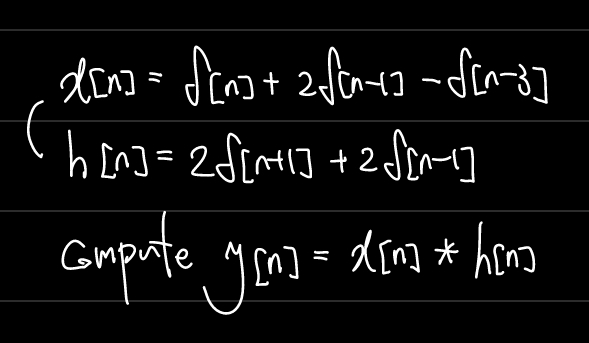
풀이
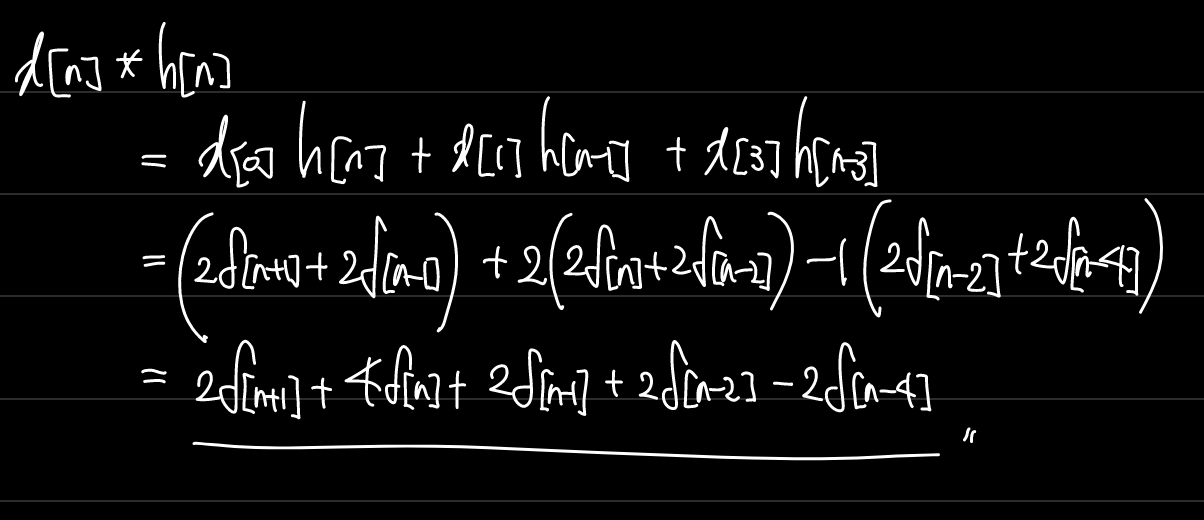
4.2 Convolution Integral의 계산 팁
Convolution Integral은 Convolution Sum의 '[방법2] n축 이용'이 불가능하다. 따라서 뒤집고 n의 범위를 적절히 나눈 뒤 곱하고 더하는(?) '[방법1] k축 이용'을 통해 계산해내야 한다.
- 물론 convolution의 성질을 이용할 수 있으면 이용하는 것이 좋다.
'전기전자 과목 | 콘텐츠' 카테고리의 다른 글
| $ e^{jkw_0t} $를 푸리에 변환하면 $ \delta(w-kw_0) $이다. (0) | 2024.10.22 |
|---|---|
| 주기함수를 푸리에 변환하면 $ \delta $가 등장한다!! | $ e^{w_0t} $ | $ cos{w_0t} $ | impulse train | Dirichlet's theorem | 혁펜하임 신호와 시스템 (0) | 2024.10.11 |
| 싱크$(sinc)$함수란? (0) | 2024.10.03 |
| 자주 쓰는 연속함수 푸리에 변환$(CTFT)$ 꼴들, 성질들 정리 (0) | 2024.10.03 |
| Duality of Fourier transform between t-domain & w-domain (0) | 2024.10.03 |