https://youtu.be/UHP-XUYvd7k?feature=shared
위 영상을 적극 참고하였다.
📖 서론
푸리에 급수의 대상은 '주기함수', 푸리에 변환의 대상은 '비주기함수'라고 배웠다.
그렇다면 '주기함수'를 푸리에 변환하면 어떻게 될까? 혹은 아예 불가능한 것인가?
위 질문에 대한 답변들을 정리해 보았다.
이 글에 나오는 푸리에 급수와 푸리에 변환은 모두 연속시간$ ( $Continuous Time$ ) %의 것들이다.
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- C-T 푸리에 급수 : 링크
- C-T 푸리에 변환 : 링크
- 디리클레 조건 : 링크
❗줄임말
- CTFS : Continous Time Fourier Series, 연속시간 푸리에 급수
- CTFT : Continous Time Fourier Transform, 연속시간 푸리에 변환
- FT : Fourier Transform, 푸리에 변환 $ ( $이 글에서는 CTFT를 의미한다.$ ) $
1. 주기함수를 FT 하는 것이 가능할까?
: 결론을 먼저 이야기하자면, FT가 가능하지만 $ \delta $가 포함된 형태이다.
$ ( $만일 \delta를 포함한 꼴을 함수로 인정하지 않는 관점을 채택한다면, 주기함수는 FT를 할 수 없다고도 할 수 있다.$ ) $
$ ( $너무 복잡해지니 그냥 '할 수 있지만 $ \delta $가 포함된다'고 생각하자..$ ) $
주기함수를 FT하기 위해서 해소해야 할 의문점은 아래 두가지와 같다.
1.1 의문점1$ ) $ FT 공식을 유도할 때, 비주기 함수를 대상으로 유도를 시작하지 않나?
: 주기 함수가 비주기 함수인 척을 할 수 있다.
예를 들어 아래와 같은 함수는 완벽한 주기 함수인데, 이를 좀 가공하여 비주기 함수로 만들어보자.
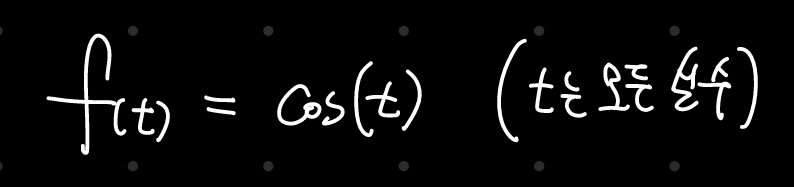
아래와 같은 g$ ( $t$ ) $는 비주기 함수가 된다.

이때 g$ ( $t$ ) $에 대하여 $ a\rightarrow\infty $를 하게 되면, 비주기적인 부분이 무한대로 밀리기 때문에 주기함수의 성질을 갖는 비주기 함수가 된다.
$ ( $정확하게 주기 함수인지, 비주기 함수인지 확신은 못하겠다... $ ) $
이런 식으로 주기함수들을 가공하여 비주기 함수로 만들어 버린다면 FT 또한 가능해진다!
$ ( $FS에서 FT 식을 유도해 낼 때에도 비슷한 가공이 쓰였었다.$ ) $
1.2 의문점2$ ) $ 주기함수는 디리클레 조건도 만족 안하는데, FT가 어떻게 가능한가?
: 디리클레 조건은 FT를 위한 '충분 조건'이다. 즉, 아래 벤다이어그램과 같은 느낌이다.

2. 주기함수의 FT를 구하는 방법
[순서1] 주기함수를 $ e^{jkw_0t} $들로 분해한다. $ ( $FS 이용$ ) $
[순서2] $ e^{jkw_0t} $의 FT가 $ \delta(w-kw_0) $임을 이용한다.
구체적인 예시를 통해 알아보자.
$ ( $ex$) $ 주기함수 $ y = cos(kw_0t) $의 FT를 구하시오.
$ ( $풀이$ ) $
[순서1] 주기함수를 $ e^{jkw_0t} $들로 분해한다. $ ( $FS 이용$ ) $
$ cos(kw_0t) = (1/2)e^{jkw_0t} +(1/2)e^{-jkw_0t} $
[순서2] $ e^{jkw_0t} $의 FT가 $ \delta(w-kw_0) $임을 이용한다.
$ (1/2)e^{jkw_0t} \rightarrow \delta(w-kw_0) $
$ (1/2)e^{-jkw_0t} \rightarrow \delta(w+kw_0) $
$ \therefore cos(kw_0t) = (1/2)e^{jkw_0t} +(1/2)e^{-jkw_0t} \rightarrow (1/2)\delta(w-kw_0) + (1/2)\delta(w+kw_0) $
'전기전자 과목 | 콘텐츠' 카테고리의 다른 글
| 이산시간 복소지수함수$ ( $D-T Complex Exponential$ ) $의 'n에 대한' 주기성 (0) | 2024.11.12 |
|---|---|
| $ e^{jkw_0t} $를 푸리에 변환하면 $ \delta(w-kw_0) $이다. (0) | 2024.10.22 |
| 컨볼루션 합$ ( $Convolution Sum$ ) $, 컨볼루션 적분$ ( $Convolution Integral$ ) $이란? | 직관적 이해 | 성질 | 계산 팁 | 계산연습문제 (1) | 2024.10.04 |
| 싱크$(sinc)$함수란? (0) | 2024.10.03 |
| 자주 쓰는 연속함수 푸리에 변환$(CTFT)$ 꼴들, 성질들 정리 (0) | 2024.10.03 |
https://youtu.be/UHP-XUYvd7k?feature=shared
위 영상을 적극 참고하였다.
📖 서론
푸리에 급수의 대상은 '주기함수', 푸리에 변환의 대상은 '비주기함수'라고 배웠다.
그렇다면 '주기함수'를 푸리에 변환하면 어떻게 될까? 혹은 아예 불가능한 것인가?
위 질문에 대한 답변들을 정리해 보았다.
이 글에 나오는 푸리에 급수와 푸리에 변환은 모두 연속시간$ ( $Continuous Time$ ) %의 것들이다.
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- C-T 푸리에 급수 : 링크
- C-T 푸리에 변환 : 링크
- 디리클레 조건 : 링크
❗줄임말
- CTFS : Continous Time Fourier Series, 연속시간 푸리에 급수
- CTFT : Continous Time Fourier Transform, 연속시간 푸리에 변환
- FT : Fourier Transform, 푸리에 변환 $ ( $이 글에서는 CTFT를 의미한다.$ ) $
1. 주기함수를 FT 하는 것이 가능할까?
: 결론을 먼저 이야기하자면, FT가 가능하지만 $ \delta $가 포함된 형태이다.
$ ( $만일 \delta를 포함한 꼴을 함수로 인정하지 않는 관점을 채택한다면, 주기함수는 FT를 할 수 없다고도 할 수 있다.$ ) $
$ ( $너무 복잡해지니 그냥 '할 수 있지만 $ \delta $가 포함된다'고 생각하자..$ ) $
주기함수를 FT하기 위해서 해소해야 할 의문점은 아래 두가지와 같다.
1.1 의문점1$ ) $ FT 공식을 유도할 때, 비주기 함수를 대상으로 유도를 시작하지 않나?
: 주기 함수가 비주기 함수인 척을 할 수 있다.
예를 들어 아래와 같은 함수는 완벽한 주기 함수인데, 이를 좀 가공하여 비주기 함수로 만들어보자.
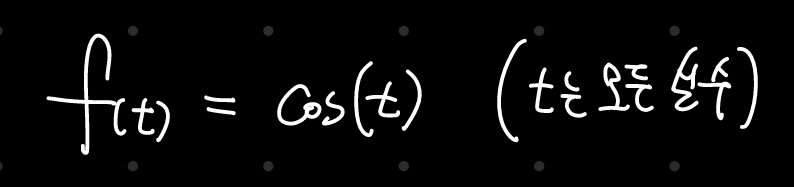
아래와 같은 g$ ( $t$ ) $는 비주기 함수가 된다.

이때 g$ ( $t$ ) $에 대하여 $ a\rightarrow\infty $를 하게 되면, 비주기적인 부분이 무한대로 밀리기 때문에 주기함수의 성질을 갖는 비주기 함수가 된다.
$ ( $정확하게 주기 함수인지, 비주기 함수인지 확신은 못하겠다... $ ) $
이런 식으로 주기함수들을 가공하여 비주기 함수로 만들어 버린다면 FT 또한 가능해진다!
$ ( $FS에서 FT 식을 유도해 낼 때에도 비슷한 가공이 쓰였었다.$ ) $
1.2 의문점2$ ) $ 주기함수는 디리클레 조건도 만족 안하는데, FT가 어떻게 가능한가?
: 디리클레 조건은 FT를 위한 '충분 조건'이다. 즉, 아래 벤다이어그램과 같은 느낌이다.

2. 주기함수의 FT를 구하는 방법
[순서1] 주기함수를 $ e^{jkw_0t} $들로 분해한다. $ ( $FS 이용$ ) $
[순서2] $ e^{jkw_0t} $의 FT가 $ \delta(w-kw_0) $임을 이용한다.
구체적인 예시를 통해 알아보자.
$ ( $ex$) $ 주기함수 $ y = cos(kw_0t) $의 FT를 구하시오.
$ ( $풀이$ ) $
[순서1] 주기함수를 $ e^{jkw_0t} $들로 분해한다. $ ( $FS 이용$ ) $
$ cos(kw_0t) = (1/2)e^{jkw_0t} +(1/2)e^{-jkw_0t} $
[순서2] $ e^{jkw_0t} $의 FT가 $ \delta(w-kw_0) $임을 이용한다.
$ (1/2)e^{jkw_0t} \rightarrow \delta(w-kw_0) $
$ (1/2)e^{-jkw_0t} \rightarrow \delta(w+kw_0) $
$ \therefore cos(kw_0t) = (1/2)e^{jkw_0t} +(1/2)e^{-jkw_0t} \rightarrow (1/2)\delta(w-kw_0) + (1/2)\delta(w+kw_0) $
'전기전자 과목 | 콘텐츠' 카테고리의 다른 글
| 이산시간 복소지수함수$ ( $D-T Complex Exponential$ ) $의 'n에 대한' 주기성 (0) | 2024.11.12 |
|---|---|
| $ e^{jkw_0t} $를 푸리에 변환하면 $ \delta(w-kw_0) $이다. (0) | 2024.10.22 |
| 컨볼루션 합$ ( $Convolution Sum$ ) $, 컨볼루션 적분$ ( $Convolution Integral$ ) $이란? | 직관적 이해 | 성질 | 계산 팁 | 계산연습문제 (1) | 2024.10.04 |
| 싱크$(sinc)$함수란? (0) | 2024.10.03 |
| 자주 쓰는 연속함수 푸리에 변환$(CTFT)$ 꼴들, 성질들 정리 (0) | 2024.10.03 |