📖 서론
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- 이산시간 함수의 기본
- 복소평면
❗줄임말
- D-T : Discrete-Time, 이산시간
1. 주기함수이기 위한 조건 $ ( $n에 대한$ ) $
이산시간 복소지수함수는 연속시간 복소지수함수보다 생각해야할 게 더 많다. 특히 1.2 부분은 이산시간 만의 독특한 조건이므로 잘 알아두어야 한다.
또한 제목에 'n에 대한'이라고 쓴 이유는 'w_0'에 대해서도 주기성이 존재하기 때문에 이를 구분하기 위함이다!!!
1.1 지수가 순허수
일반적인 이산시간 복소지수함수는 아래와 같이 생겼다. C와 a가 모두 복소수이다.

위 꼴이 주기함수가 되기 위해서는 지수에 있는 a가 '순허수'가 되어야 한다.
만약 a = 3 + 2j 같은 순허수가 아닌 복소수라면, 3이라는 실수값에 의해 n이 증가함에 따라 진폭의 성장이 생긴다. 즉 진폭 때문에 y[n+N] = y[n]의 등호가 성립하기 힘들다.
- C는 실수, 순허수, 순허수가 아닌 허수건 뭐든 상관 없다. 물론 $ w_0 $는 실수여야 한다.

1.2 주파수의 조건
1.1에서 $ ( $e^{jw_0n}$ ) $의 꼴이 주기성을 가질 '수' 있다고 하였다. $ ( $w_0$ ) $의 조건에 따라 이 함수가 주기함수일 수도 있고 아닐 수도 있다.
연속시간에서는 지수가 순허수면 무조건 주기성을 띄고, $ w_0 $의 절댓값이 커질수록 주기도 짧아지지만, 이산시간에서는 이렇게 간단하지 않다.
$ ( $이산시간이 좀 더 까다롭다...$ ) $
주파수를 먼저 정리해두는게 좋을 것 같다. 지수에서 j와 n에 끼어 있는 부분이 주파수이고, 통상 $ ( $w_0$ ) $으로 표현한다. 아래의 빨간 네모 자리에 해당하는게 '주파수' 라고 생각하는게 좋다.
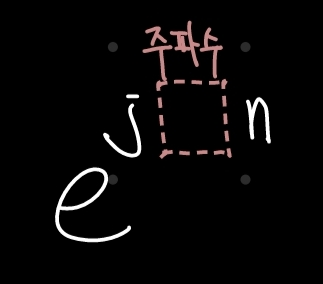
위 함수가 n에 대하여 주기함수가 되기 위해서는,
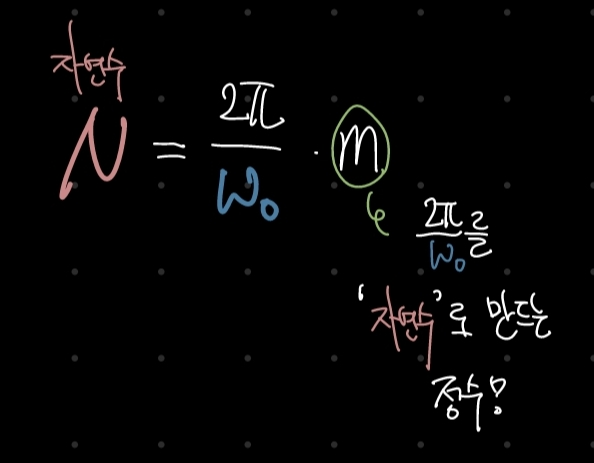
위 식을 만족하는 정수 m이 존재해야 한다. 예를 들어,
- $ w_0 = \pi / 3 $면은 m=1을 이용하여 N=6을 만들 수 있어서 주기함수이다.
- $ w_0 = 3 $이면 $ {2\pi}/w_0 = 2\pi/3 $가 무리수이므로 어떤 정수 m을 가져와도 N을 자연수로 만들 수 없다. 즉 주기함수가 아니다.
참고로 자연수 N이 존재한다면, 가능한 가장 작은 N이 그 함수의 주기이다.
2. 주파수가 클수록 주기가 짧다?
연속시간 복소지수함수에서는 주파수가 클수록 주기 T 값이 짧아진다.
연속시간에서는 $ T = 2\pi / w_0 $ 로 간단히 표현된다. T와 $ w_0 $가 반비례 관계에 있음이 직관적으로 잘 보인다.
하지만 이산시간 복소지수함수에서는 상관 관계가 없는 것 같다. 아래의 예시를 보면 주파수가 커질수록 N=6, 21, 14로 짧아지는 경향성이 보이지 않는다.

'전기전자 과목 | 콘텐츠' 카테고리의 다른 글
| SR Latch의 기본 정보 | 논리 게이트로 구현 (0) | 2024.11.17 |
|---|---|
| delta train의 DTFT 구하기 (1) | 2024.11.13 |
| $ e^{jkw_0t} $를 푸리에 변환하면 $ \delta(w-kw_0) $이다. (0) | 2024.10.22 |
| 주기함수를 푸리에 변환하면 $ \delta $가 등장한다!! | $ e^{w_0t} $ | $ cos{w_0t} $ | impulse train | Dirichlet's theorem | 혁펜하임 신호와 시스템 (0) | 2024.10.11 |
| 컨볼루션 합$ ( $Convolution Sum$ ) $, 컨볼루션 적분$ ( $Convolution Integral$ ) $이란? | 직관적 이해 | 성질 | 계산 팁 | 계산연습문제 (1) | 2024.10.04 |
📖 서론
[신호와 시스템] 공부를 위한 목차 및 색인 $ ( $주제별 링크 + 단원별 정리 + 공부에 도움되는 자료들$ ) $
💬 배경지식
- 이산시간 함수의 기본
- 복소평면
❗줄임말
- D-T : Discrete-Time, 이산시간
1. 주기함수이기 위한 조건 $ ( $n에 대한$ ) $
이산시간 복소지수함수는 연속시간 복소지수함수보다 생각해야할 게 더 많다. 특히 1.2 부분은 이산시간 만의 독특한 조건이므로 잘 알아두어야 한다.
또한 제목에 'n에 대한'이라고 쓴 이유는 'w_0'에 대해서도 주기성이 존재하기 때문에 이를 구분하기 위함이다!!!
1.1 지수가 순허수
일반적인 이산시간 복소지수함수는 아래와 같이 생겼다. C와 a가 모두 복소수이다.

위 꼴이 주기함수가 되기 위해서는 지수에 있는 a가 '순허수'가 되어야 한다.
만약 a = 3 + 2j 같은 순허수가 아닌 복소수라면, 3이라는 실수값에 의해 n이 증가함에 따라 진폭의 성장이 생긴다. 즉 진폭 때문에 y[n+N] = y[n]의 등호가 성립하기 힘들다.
- C는 실수, 순허수, 순허수가 아닌 허수건 뭐든 상관 없다. 물론 $ w_0 $는 실수여야 한다.

1.2 주파수의 조건
1.1에서 $ ( $e^{jw_0n}$ ) $의 꼴이 주기성을 가질 '수' 있다고 하였다. $ ( $w_0$ ) $의 조건에 따라 이 함수가 주기함수일 수도 있고 아닐 수도 있다.
연속시간에서는 지수가 순허수면 무조건 주기성을 띄고, $ w_0 $의 절댓값이 커질수록 주기도 짧아지지만, 이산시간에서는 이렇게 간단하지 않다.
$ ( $이산시간이 좀 더 까다롭다...$ ) $
주파수를 먼저 정리해두는게 좋을 것 같다. 지수에서 j와 n에 끼어 있는 부분이 주파수이고, 통상 $ ( $w_0$ ) $으로 표현한다. 아래의 빨간 네모 자리에 해당하는게 '주파수' 라고 생각하는게 좋다.

위 함수가 n에 대하여 주기함수가 되기 위해서는,
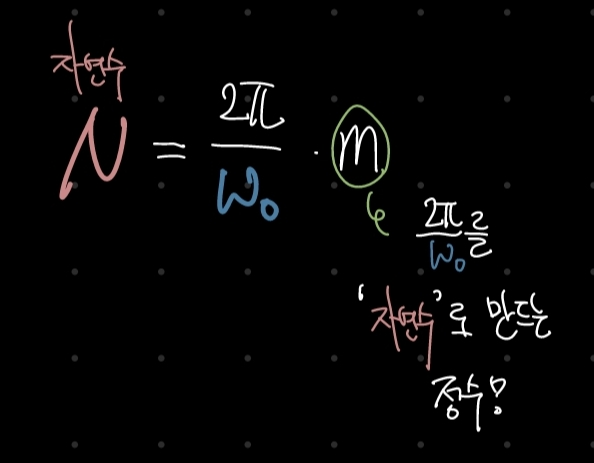
위 식을 만족하는 정수 m이 존재해야 한다. 예를 들어,
- $ w_0 = \pi / 3 $면은 m=1을 이용하여 N=6을 만들 수 있어서 주기함수이다.
- $ w_0 = 3 $이면 $ {2\pi}/w_0 = 2\pi/3 $가 무리수이므로 어떤 정수 m을 가져와도 N을 자연수로 만들 수 없다. 즉 주기함수가 아니다.
참고로 자연수 N이 존재한다면, 가능한 가장 작은 N이 그 함수의 주기이다.
2. 주파수가 클수록 주기가 짧다?
연속시간 복소지수함수에서는 주파수가 클수록 주기 T 값이 짧아진다.
연속시간에서는 $ T = 2\pi / w_0 $ 로 간단히 표현된다. T와 $ w_0 $가 반비례 관계에 있음이 직관적으로 잘 보인다.
하지만 이산시간 복소지수함수에서는 상관 관계가 없는 것 같다. 아래의 예시를 보면 주파수가 커질수록 N=6, 21, 14로 짧아지는 경향성이 보이지 않는다.

'전기전자 과목 | 콘텐츠' 카테고리의 다른 글
| SR Latch의 기본 정보 | 논리 게이트로 구현 (0) | 2024.11.17 |
|---|---|
| delta train의 DTFT 구하기 (1) | 2024.11.13 |
| $ e^{jkw_0t} $를 푸리에 변환하면 $ \delta(w-kw_0) $이다. (0) | 2024.10.22 |
| 주기함수를 푸리에 변환하면 $ \delta $가 등장한다!! | $ e^{w_0t} $ | $ cos{w_0t} $ | impulse train | Dirichlet's theorem | 혁펜하임 신호와 시스템 (0) | 2024.10.11 |
| 컨볼루션 합$ ( $Convolution Sum$ ) $, 컨볼루션 적분$ ( $Convolution Integral$ ) $이란? | 직관적 이해 | 성질 | 계산 팁 | 계산연습문제 (1) | 2024.10.04 |